Charles L. Kane, Andrew M. Rappe and Eugene J. Mele
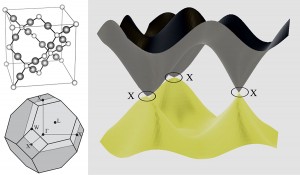
A three dimensional Dirac Semimetal: (a) Crystal structure and (b) Brillouin zone of newly proposed material, BiO2 in the β-cristobalite structure. (c) shows the map of energy vs. momentum for BiO2, which exhibits linear dispersion and Dirac points at the Fermi energy at the X points in the Brillouin zone. This band structure can be viewed as a three-dimensional generalization of graphene.
Graphene has captured the imagination of scientists around the world because of its unique two-dimensional electronic structure, in which the conduction and valence bands touch each other at isolated points in momentum space, known as “Dirac points”. Motivated by our progress in the understanding of topological band theory–which led to the discovery of three-dimensional topological insulators–we ask whether similar physics could arise in three-dimensional materials. The answer is yes, though there are some interesting twists to the story.
We have introduced the concept of a “Dirac Semimetal”, a three-dimensional material where the conduction and valence bands meet at points and are described by a three-dimensional Dirac equation. We have carefully elucidated the rather non-trivial symmetry requirements for such a Dirac semimetal to exist, and we have initiated a systematic search for real materials that exhibit this phase. Based on ab initio electronic structure calculations, we have predicted that BiO2 in the metastable b-cristobalite phase is a Dirac semimetal, and that it has three symmetry-related Dirac points at the Fermi energy. This leads to a three-dimensional generalization of graphene, and it is expected to exhibit novel electronic transport properties, such as a high electron mobility.
