Tom Lubensky, Andrea Liu, Arjun Yodh, Shu Yang and Ju Li
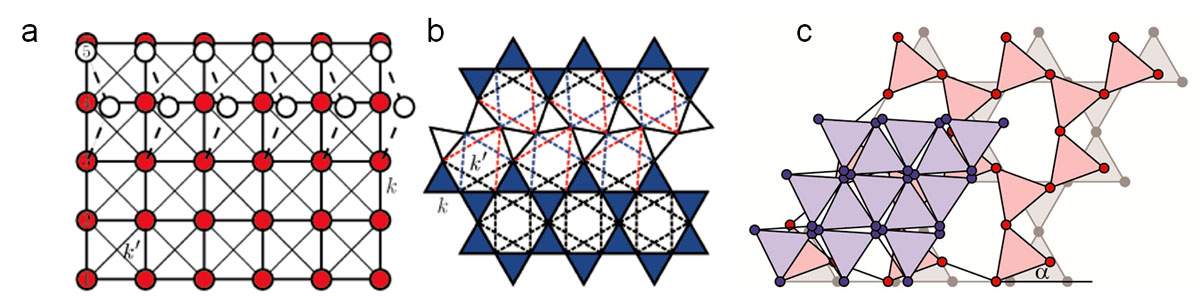
Fig. 1. (a) Square and (b) kagome lattices with NN springs of spring constant k and NNN springs of spring constant k’. White circles in (a) and white triangles in (b) show a zero-energy distortion. (c) A sequence of twisted kagome lattices. Pulling the purple lattice along the horizontal axis cause it to expand in both the horizontal and vertical directions to the pink and grey lattices, the defining characteristic of auxetic materials. Twisted kagome lattices with triangles at angle a to horizontal.
An isostatic lattice is one at the threshold of mechanical stability. The square and kagome lattices (see Figure 1a-b) in two dimensions are examples of isostatic lattices. A 2D kagome lattice of N sites has of order N1/2 zero-energy bulk modes under periodic boundary conditions. Theoretical study shows that when neighboring triangles are counter rotated through an arbitrary angle α shown in Figure 1c, the bulk modulus vanishes, making the Poisson’s ratio equal to -1, and all of the bulk zero modes of the α =0 lattice disappear. The study of rigidity and its restoration in these lattices as a function of bending forces or next-nearest-neighbor springs will improve our understanding of jamming of hard spheres systems and of networks of semi-flexible polymers, and offer new paradigms for the microscopic mechanics of disordered media. Taking the general concept of network nstability, we expect to develop a new opto-mechano based materials platform to dynamically tune the photonic and phononic properties.
